Delta
Delta is a theoretical estimate of how much an option’s premium may change given a $1 move in the underlying. For an option with a Delta of .50, an investor can expect about a $.50 move in that option’s premium given a $1 move, up or down, in the underlying. For purchased options owned by an investor, Delta is between 0 and 1.00 for calls and 0 and -1.00 for puts. For sold options, as the investor essentially has a negative quantity of contracts, we find that short puts have a positive Delta (technically a negative Delta multiplied by a negative number of contracts); short calls have negative Delta (technically a positive Delta times a negative number of contracts).
For example, with stock trading at $20.50, a $20 call option might be trading for a quoted premium of $2 and an option Delta of .50. If share prices rise $1 to $21.50, it would be expected for the value of the option to increase to $2.50 all other pricing factors remaining constant. As seen below:
- $1 increase in underlying price x .50 Delta = $.50 anticipated change in option premium.
- Original Premium: $2.00 + $.50 estimated change = $2.50 estimated new premium after $1 stock price increase.
If share prices fall by $1, this same $20 call option would be expected to lose $.50 in value, all other pricing factors remaining constant.
As the stock price rises and the call option goes deeper-in-the-money, Delta typically approaches 1.00 because of the increased likelihood the option will be in-the-money at expiration. As expiration approaches, in-the-money-option Deltas are also more likely to be moving slowly toward 1.00 because at expiration an option either has a Delta of either 0 or 1.00 with no time premium remaining.
Here is a look at a call Delta and how it might move:
- On a given day, an OICX call has a Delta of .50 (50%)
- Current value $3.50
- OICX stock goes up $1:
- Call will theoretically increase by 50% of stock move
- $1.00 x .50 = $.50
- Expected call value = $3.50 current + $.50 = $4.00
- OICX stock goes up $.60:
- Call will theoretically increase by $.60 x .50 = $0.30
- Expected call value = $3.50 current + $.30 = $3.80
The following graph illustrates how Delta might be plotted against stock price:
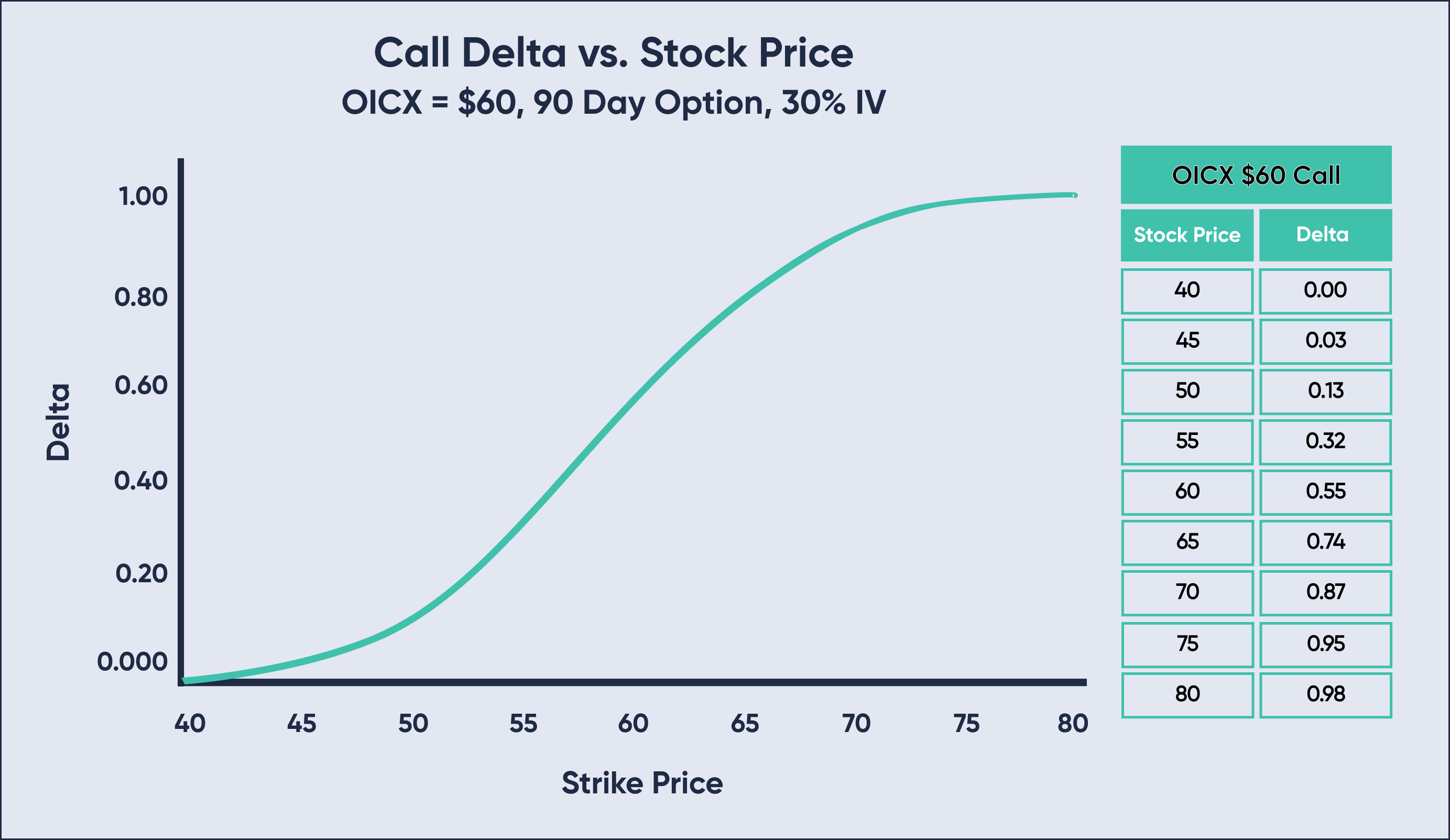
Call Deltas range from 0.00 to 1.00 while put Delta ranges from 0.00 to -1.00. Remember long calls have positive Delta; conversely short calls have negative Delta. Long puts have negative Delta; short puts have positive Delta. The closer an option's Delta is to 1.00 or -1.00, the more the price of the option responds (in terms of dollars) to actual long or short stock when the underlying moves. Here is a quick chart for reference:
- Calls have positive Deltas (as generated by model)
- Positive correlation to underlying stock price change
- Stock price ↑ then call Delta tends to go up ↑
- Stock price ↓ then call Delta tends to go ↓
- Call Deltas range from 0 to +1.00
- Puts have negative Deltas (as generated by model)
- Negative correlation to underlying stock price change
- Stock price ↑ then put Delta tends to go ↓
- Stock price ↓ then put Delta tends to go ↑
- Put Deltas range from 0 to –1.00
Stock price, days remaining to expiration and implied volatility will impact Delta. With an increase in implied volatility, Delta gravitates toward .50 as more and more strikes are now considered possibilities for winding up in-the-money because of the perceived potential for movement in the underlying. For example, the 20 strike call in XYZ may have a .60 Delta with the stock at $21 and implied volatility at 30%. If implied volatility were to increase to 40%, the Delta may decrease to .55 as traders perceive an increased likelihood that the strike might be out-of-the-money at expiration.
Here is a look at how implied volatility changes can alter Delta:
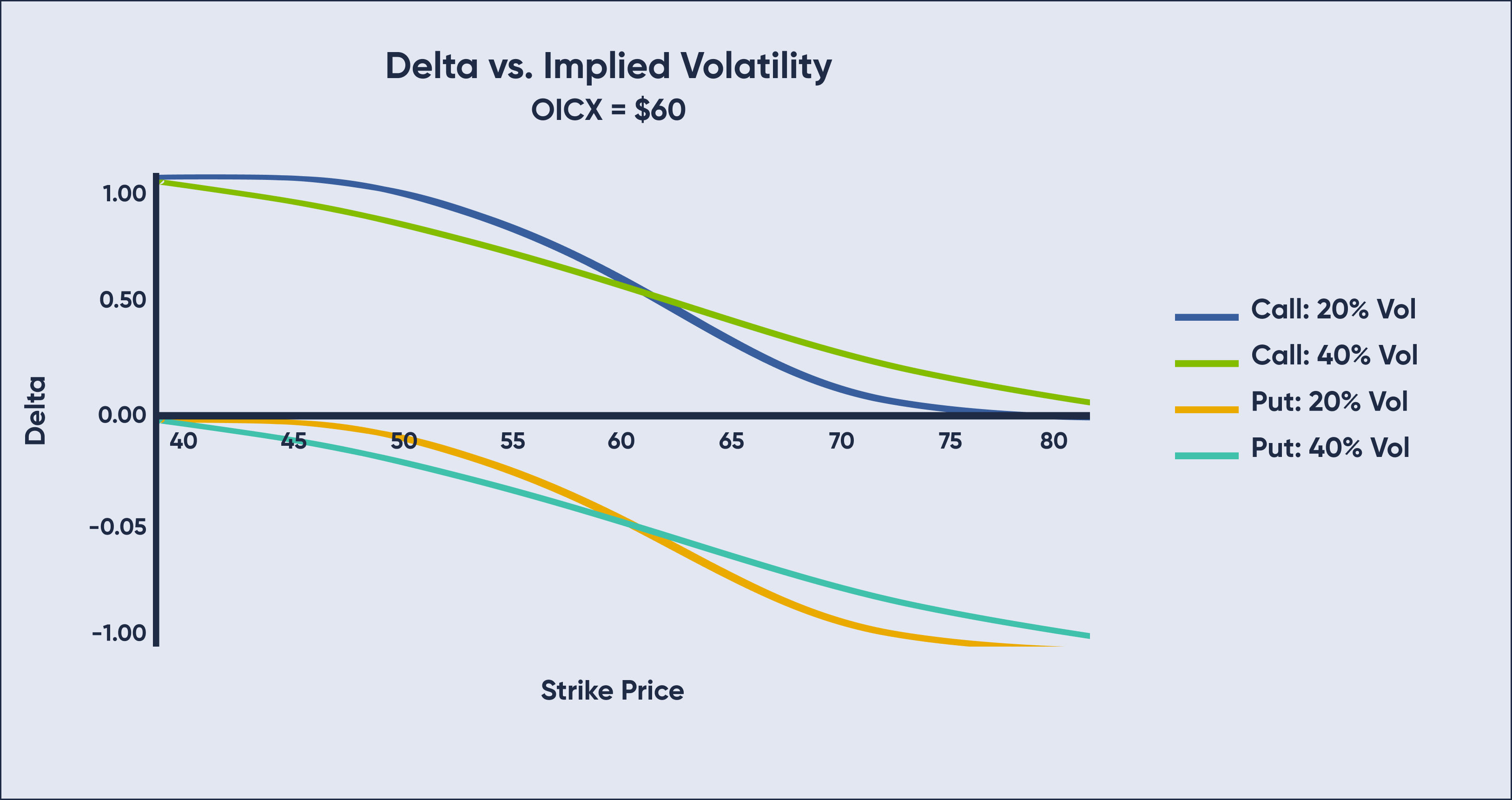
Above we can see that higher implied volatilities lead to more strikes being ‘in play’ and more Deltas closer to .50. Low implied volatility stocks will tend to have higher Delta for the in-the-money options and lower Delta for out-of-the-money options.
Some traders view Delta as a percentage probability an option will wind up in-the-money at expiration. Therefore, an at-the-money option would have a .50 Delta or 50% chance of being in-the-money at expiration. Deep-in-the-money options will have a much larger Delta or much higher probability of expiring in-the-money.
Looking at the Delta of a far-out-of-the-money option might give an investor an idea of its likelihood of having value at expiration. An option with less than a .10 Delta (or less than 10% probability of being in-the-money) is not viewed as very likely to be in-the-money at any point and will need a strong move from the underlying to have value at expiration.
Time remaining until expiration will also have an effect on Delta. Looking at the same strike, an in-the-money call with longer time until expiration will always have a lower Delta than the same strike call with less time until expiration. It is just the opposite for out-of-the-money calls; the call with a longer amount of time until expiration will have the higher Delta than the option with less time.
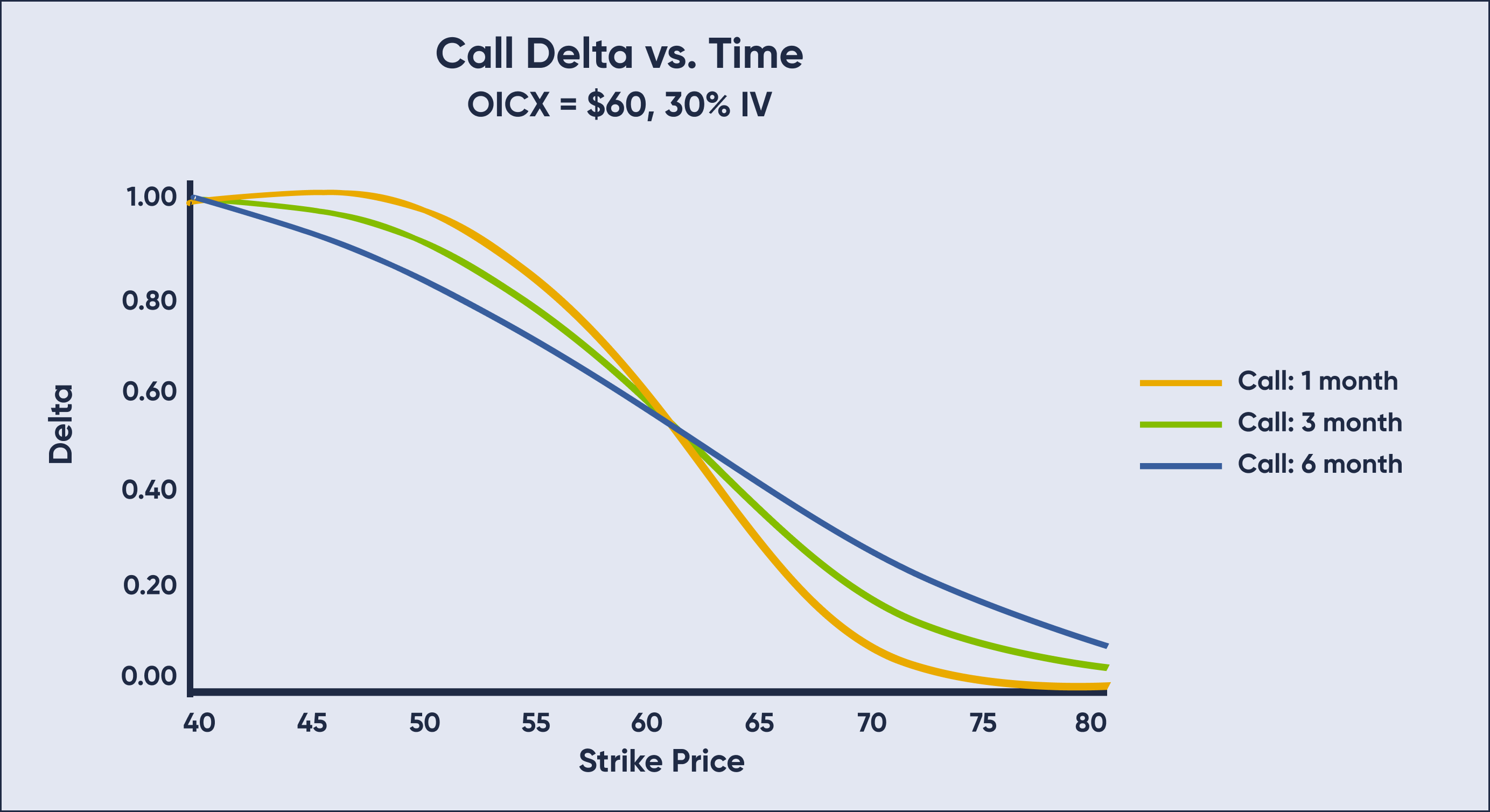
As expiration nears, in-the-money call Deltas increase toward 1.00, at-the-money call Deltas remain around .50 and out-of-the-money call Deltas fall toward 0 provided other inputs remain constant.
It is important to remember that Delta is constantly changing during market hours and will typically not accurately predict the exact change in an option’s premium.

