Options Pricing
An option’s premium has two main components: intrinsic value and time value.
Intrinsic Value (Calls)
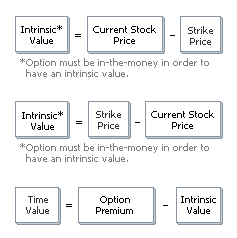
A call option is in-the-money when the underlying security's price is higher than the strike price.
Intrinsic Value (Puts)
A put option is in-the-money if the underlying security's price is less than the strike price. Only in-the-money options have intrinsic value. It represents the difference between the current price of the underlying security and the option's exercise price, or strike price.
Time Value
Time value is any premium in excess of intrinsic value before expiration. Time value is often explained as the amount an investor is willing to pay for an option above its intrinsic value. This amount reflects hope that the option’s value increases before expiration due to a favorable change in the underlying security’s price. The longer the amount of time available for market conditions to work to an investor's benefit, the greater the time value.
Major Factors Influencing Options Premium
Factors having a significant effect on options premium include:
- Underlying price
- Strike
- Time until expiration
- Implied volatility
- Dividends
- Interest rate
Dividends and risk-free interest rate have a lesser effect.
Changes in the underlying security price can increase or decrease the value of an option. These price changes have opposite effects on calls and puts. For instance, as the value of the underlying security rises, a call will generally increase. However, the value of a put will generally decrease in price. A decrease in the underlying security's value generally has the opposite effect.
The strike price determines whether an option has intrinsic value. An option's premium (intrinsic value plus time value) generally increases as the option becomes further in-the-money. It decreases as the option becomes more deeply out-of-the-money.
Time until expiration, as discussed above, affects the time value component of an option's premium. Generally, as expiration approaches, the levels of an option's time value decrease or erode for both puts and calls. This effect is most noticeable with at-the-money options.
The effect of implied volatility is subjective and difficult to quantify. It can significantly affect the time value portion of an option's premium. Volatility is a measure of risk (uncertainty), or variability of price of an option's underlying security. Higher volatility estimates indicate greater expected fluctuations (in either direction) in underlying price levels. This expectation generally results in higher option premiums for puts and calls alike. It is most noticeable with at-the-money options.
The effect of an underlying security's dividends and the current risk-free interest rate has a small but measurable effect on option premiums. This effect reflects the cost to carry shares in an underlying security. Cost of carry is the potential interest paid for margin or received from alternative investments (such as a Treasury bill) and the dividends from owning shares outright. Pricing takes into account an option’s hedged value so dividends from stock and interest paid or received for stock positions used to hedge options are a factor.
Please visit our learning resources by topic pages to learn more about Options Pricing.

